|
|
. |
|
.
|
LINEAS DE
INVESTIGACION |
Los servomecanismos constituyen un componente fundamental en el funcionamiento de diferentes tipos de plataformas robóticas tales como manipuladores, robots móviles y bípedos, robots aéreos y marinos y robots domésticos entre otros. Otros equipos que emplean servomecanismos incluyen máquinas herramientas, posicionadores de antenas y de módulos fotovoltáicos, automóviles eléctricos e híbridos, sistemas fly-by wire, sistemas de corte industrial e impresoras, por nombrar algunos.
Un servomecanismo está constituido por algún tipo de motor, el cual puede rotar o tener un desplazamiento rectilíneo, sensores de posición y/o velocidad, un mecanismo de realimentación y un controlador el cual permite controlar la posición o la velocidad del motor. El motor puede acoplarse a su carga de manera directa o a través de un mecanismo de transmisión. La figura siguiente muestra un diagrama de bloques de un servomecanismo controlado en posición.
ESQUEMA BASICO DE UN SERVOMECANISMO CONTROLADO EN POSICION
La investigación que se lleva a cabo en este tema consiste en en desarrollo de leyes de control que compensen fricción mecánica, incertidumbres paramétricas y perturbaciones acotadas. Otros tópicos tales como el desarrollo de controladores no lineales también han sido estudiados.
REFERENCIAS:
1. R.A. Garrido, A. Soria-López.
Control of a servomechanism using non-linear damping.
Proceedings of the
Institution of Mechanical Engineers, Part I:
Journal of Systems and Control Engineering.
(2005), Vol. 19, No. 4,
295–299.
2. R. Garrido, D. Calderon and A. Soria.
Servomotor velocity tracking
using adaptive fuzzy techniques.
Journal of Intelligent &
Fuzzy Systems. (2009), Vol. 20, No. 4,
pp 1-9.
3. Carlos Aguilar-Ibañez,
Ruben Garrido-Moctezuma, Jorge Dávila.
Output feedback trajectory
stabilization of the uncertainty DC
servomechanism system.
ISA Transactions. (2012),
Vol. 51, No. 6, pp 801-807.
4. Carlos Aguilar-Ibañez, Julio
Mendoza-Mendoza, Jorge Davila, Miguel S.
Suarez-Castanon and Ruben Garrido M.
A robust controller for
trajectory tracking of a DC motor pendulum
system.
International Journal of
Control, Automation and Systems. (2017),
Vol. 15, No. 4, pp 1632-1640.
La identificación o ajuste de los parámetros del modelo de una planta es un aspecto fundamental en la simulación y diseño de controladores. Entre los métodos más conocidos se encuentra los algoritmos de Mínimos Cuadrados y Gradiente.
La investigación en este tópico se ha centrado en el desarrollo de técnicas de identificación paramétrica aplicadas a servomecanismos. En particular se han desarrollado métodos capaces de identificar un modelo de cuatro parámetros de un servomecanismo en lazo cerrado cuyo esquema se ilustra en la figura siguiente:
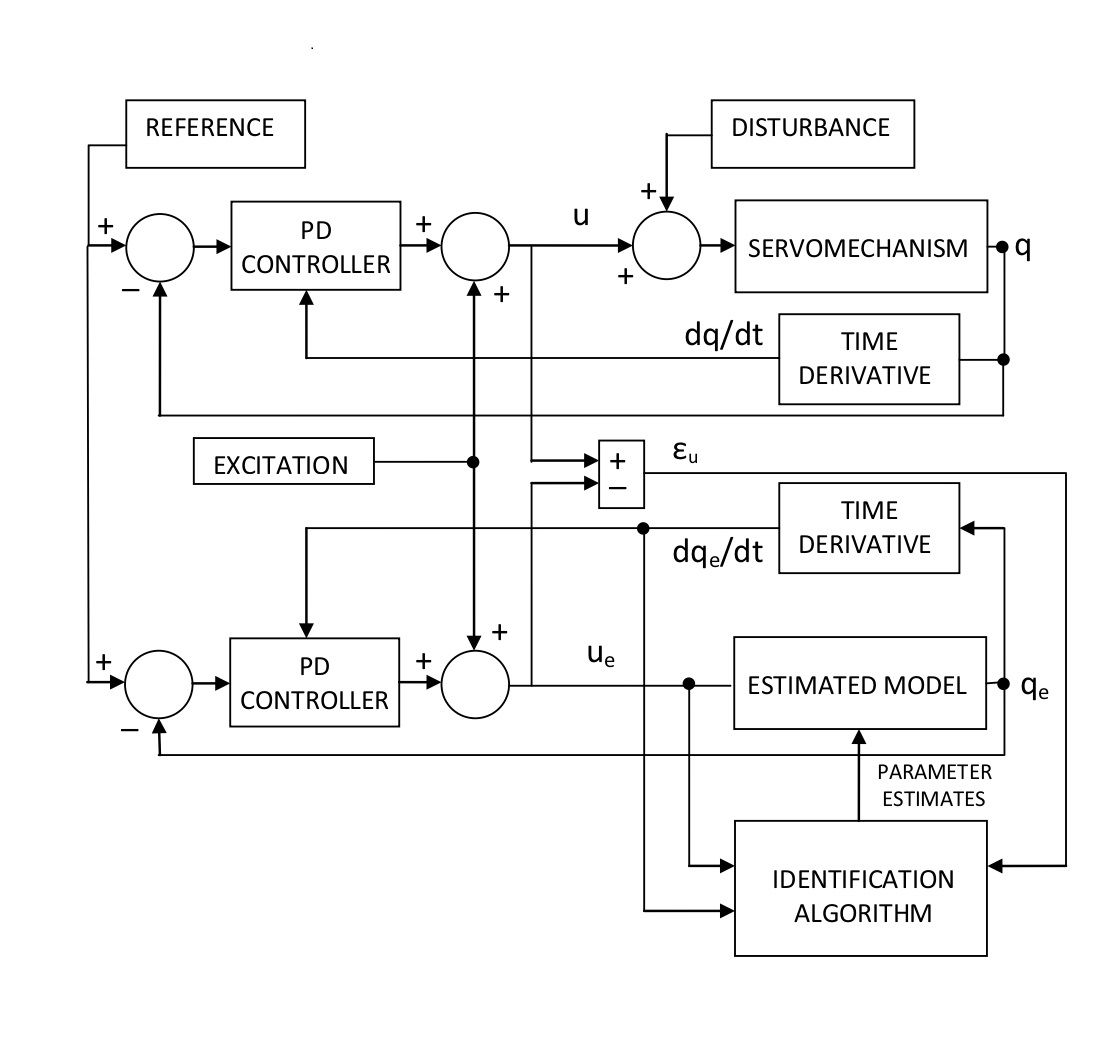
Otro método propuesto permite identificar la inercia, el coeficiente de fricción viscosa y el coeficiente de fricción de Coulomb. Además, se ha iniciado el estudio de algoritmos de optimización heurísticos como identificadores de parámetros, en particular el denominado Optimización por Enjambre de Partículas.
REFERENCIAS
1. C. Aguilar-Ibañez, J. Sánchez H., Miguel S. Suárez C., Fortunato Flores, R. Martínez Guerra, R. Garrido M.
Reconstructing and identifying the Rossler’s system by using a high gain observer.
Asian Journal of Control. (2006), Vol. 8, No. 4, pp 401-407.
2.Carlos Aguila-Ibánez, Jorge Sánchez Herrera, Rubén Garrido-Moctezuma.
Parametric estimation of the Duffing system by using a modified gradient algorithm.
Physics Letters A. (2008), Vol. 372, No. 3, pp 210-214.
3. Ruben Garrido, Roger Miranda.
DC servomechanism parameter identification: A closed loop input error approach.
ISA Transactions. (2012), Vol. 51, pp 42-49.
4.Rubén Garrido and Antonio Concha.
An Algebraic Recursive method for parameter identification of a Servo model.
IEEE/ASME Transactions on Mechatronics. (2013), Vol. 18, No. 5, pp 1572-1580.
5.Ruben Garrido, Antonio Concha.
Inertia and friction estimation of a velocity controlled servo using position measurements.
IEEE Transactions on Industrial Electronics. (2014), Vol.61, No. 9, pp 4759-4770.
6. Antonio Concha, Rubén Garrido.
Parameter estimation of the FitzHugh-Nagumo neuron model using integrals over finite time periods.
Journal of Computational and Nonlinear Dynamics. (2015), Vol. 10, No. 2, pp (020123-1)-(020123-6).
7.Antonio Concha, Luis Alvarez-Icaza, Rubén Garrido.
Simultaneous parameter and state estimation of shear buildings.
Mechanical Systems and Signal Processing. (2016), Vol. 70-71, pp 788-810.
8.Antonio Concha, Rubén Garrido, Luis Alvarez-Icaza.
Identification of shear buildings using an instrumental variable method and linear integral filters.
Journal of Sound and Vibration. (2016), Vol. 385, pp 149-170.
Uno de los aspectos fundamentales dentro del aprendizaje del Control Automático, la Robótica y la Mecatrónica es la evaluación de algoritmos de control. Esta tarea se puede llevar a cabo mediante simulaciones numéricas o a través de la utilización de prototipos de laboratorio. En el caso de éstos últimos, existen dos posibilidades para tener acceso a ellos. La primera es su compra y la segunda consiste en su construcción.
La investigación llevada a cabo sobre la construcción de prototipos está guiada por los siguientes criterios:
- Costo bajo.
- Disponibilidad de los componentes.
- Empleo de programas comerciales tales como MATLAB® o de lenguajes de programación para implementar los algoritmos de control.
- Modelos matemáticos preferente lineales que describan al prototipo.
Actualmente se tiene desarrollado un prototipo construido a partir de un servomotor de Radio Control (RC). En la elección de este último se ha tomado en cuenta su amplia disponibilidad y bajo costo.

Servomotor de RC
Para construir el prototipo se elimina la tarjeta de control alojada dentro del servomotor y se mantienen el tren de engranajes, el potenciómetro que mide la posición angular del eje de salida de este tren, el motor de Corriente Directa (CD) y la estructura del servomotor.


Vista interna del servomotor de RC con y sin tarjeta de control.

Conexiones al motor de CD y al potenciómetro.
Para alimentar al motor CD se utiliza un amplificador operacional de potencia como se muestra a continuación:
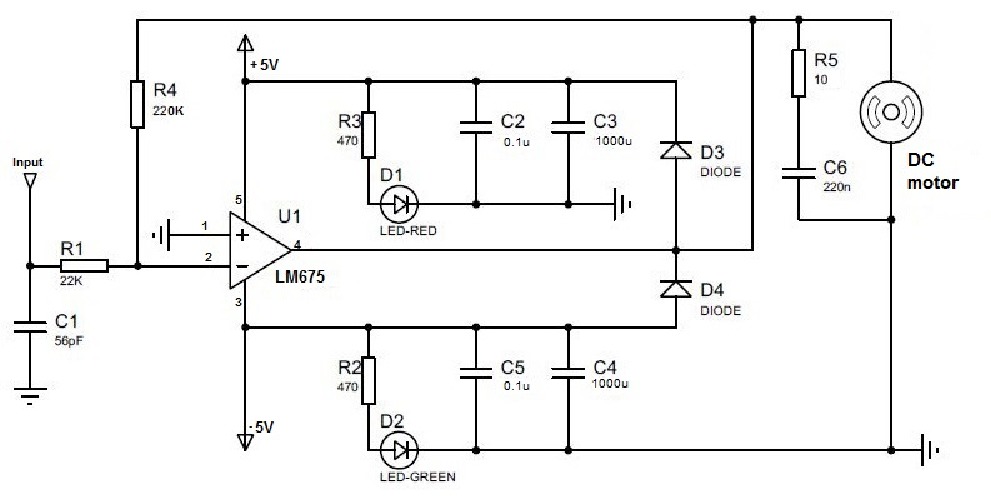
Circuito amplificador de potencia para alimentar al motor de CD basado en el amplificador operacional LM675.
El potenciómetro se utliza como un divisor de tensión para obtener un voltaje proporcional a su posición angular:

Potenciómetro y su conexión mecánica al tren de engranajes y su empleo como divisor de tensión.
Se muestra a continuación una imagen del prototipo construido incluyendo las fuentes de alimentación que utiliza:

1. J. Luis Luna, Jessica Maldonado, Rubén Garrido.
Active Disturbance Rejection Control Applied to a Low-Cost Educational Prototype.
Proceedings of the XVIII Latin American Conference in Automatic Control CLCA 2018.
Quito, Ecuador, 24 a 26 de octubre (2018): 93-94.
2.Jessica Maldonado, Rubén Garrido, Gerardo Castro.
A Methodology to Teach Mechatronics through Building a Hands-on Platform.
15th International Conference on Electrical Engineering, Computing Science and Automatic Control CCE.
Ciudad de México, México, 5 a 7 de septiembre (2018).
Este tópico ha recibido gran interés en los últimos años como lo puede atestiguar la gran cantidad de trabajos sobre el mismo. La idea básica de este esquema es realizar la estimación de la perturbación y utilizar el estimado dentro de una ley de control con el fin de contrarrestar sus efectos.
Las perturbaciones internas o externas, incertidumbres paramétricas y términos de alto orden en una expansión en series de Taylor de un modelo no lineal de la planta a controlar, se concentran en un sólo término el cual se considera como una perturbación única. La parte de la planta que no se incluyen dentro de la perturbación constituye su modelo nominal. Como ejemplo, considérese la planta siguiente la cual está constituida por varios integradores conectados en cascada
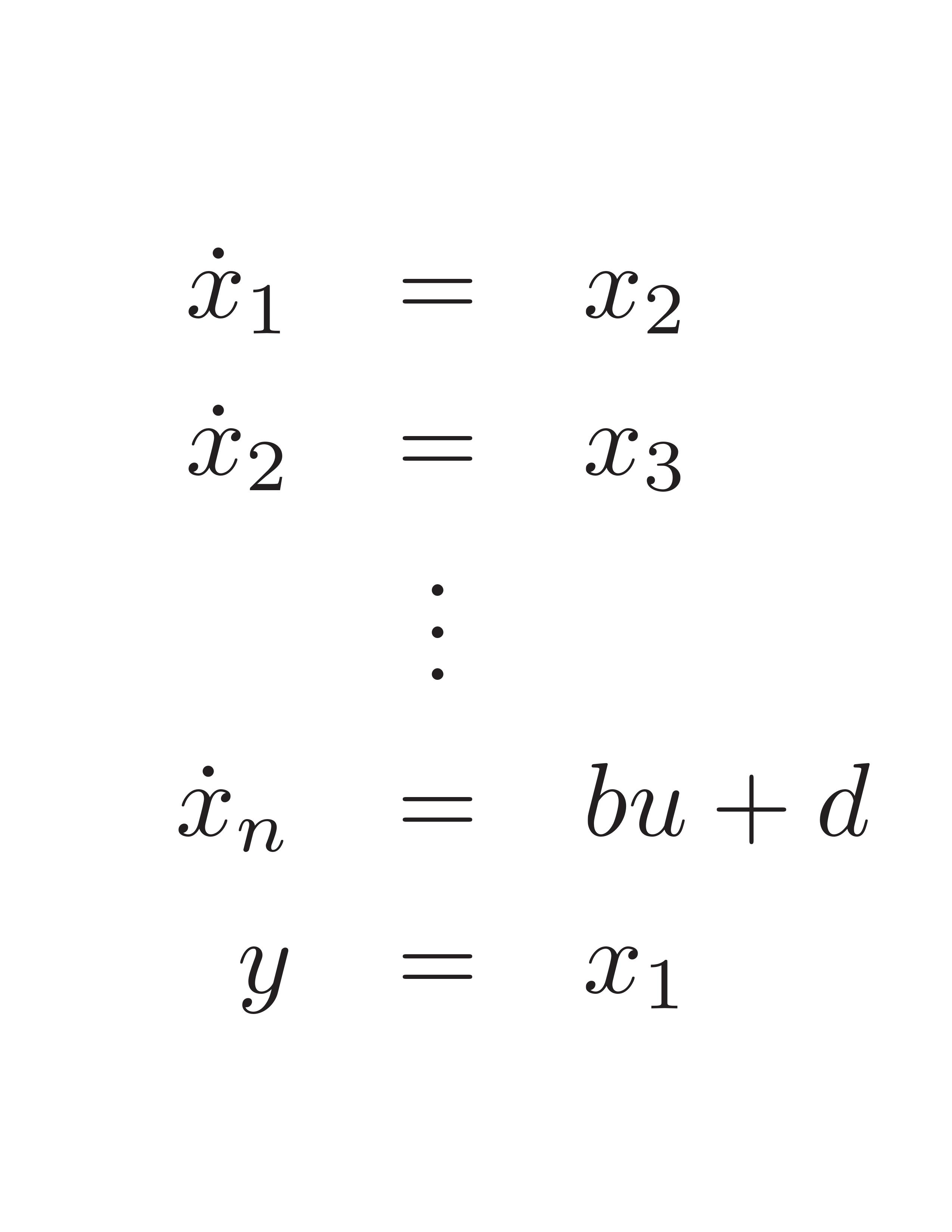
En este caso d constituye la perturbación, y la salida, xi : i=1,...,n el estado, u la entrada y b la ganancia de entrada.
Dos aspectos bajo estudio en este tema son:
- La
equivalencia
entre un
controlador
basado
en un
observador de
perturbaciones
y un
controlador
PID.
- Aplicación de observadores de incertidumbre al control de Motores Ultrasónicos Lineales (Linear Ultrasonic Motors LUM en inglés). La figura siguiente muestra a un motor de este tipo y el equipo para controlarlo.

1.Mario Ramirez-Neria, Hebertt Sira-Ramirez, Ruben Garrido-Moctezuma, Alberto Luviano-Juarez.
Linear Active Disturbance Rejection Control of Underactuated Systems: The case of the Furuta Pendulum.
ISA Transactions. (2014), Vol. 53, No. 4, pp 920-928.
2.Mario Ramirez-Neria, Hebertt Sira-Ramirez, Ruben Garrido-Moctezuma, Alberto Luviano-Juarez.
On the Linear Control of Underactuated Nonlinear systems via tangent Flatness and Active Disturbance Rejection Control:
The case of the ball and beam system.
ASME Journal of Dynamic Systems, Measurement and Control. (2016), Vol. 138, No. 10, pp (104501-1)-(104501-5).
3.M. Ramírez-Neria, H. Sira-Ramírez, R. Garrido-Moctezuma and A. Luviano-Juárez.
Active Disturbance Rejection Control of the Inertia Wheel Pendulum through a Tangent Linearization Approach.
International Journal of Control, Automation and Systems. (2019), Vol. 17, No. 1, pp 18-28.
4. Rubén Garrido, J. Luis Luna. On the equivalence between PD+DOB and PID controllers applied to servo drives.
3rd IFAC Conference on Advances in Proportional-Integral-Derivative Control,
Ghent, Belgica, 9 a 11 de mayo (2018): 95-100.
5.Carlos Aguilar-Ibanez, Hebertt Sira-Ramirez, Miguel S. Suarez-Castanon and Ruben Garrido.
Robust trajectory tracking control of a PVTOL under crosswinds.
Asian Journal of Control. (2019), Vol. 21, No. 3, pp 1293-1306.
Los sistemas de seguimiento juegan un papel importante en el aprovechamiento de la energía solar, en particular, en el caso de celdas fotovoltaicas de concentración. El seguimento del movimiento aparente del sol puede realizarse utilizando los esquemas siguientes:
La figura siguiente muestra un seguidor solar de dos ejes
El esquema de laboratorio siguiente se ha utilizado para llevar a cabo experimentos con un seguidor de un eje.
REFERENCIAS
1.
Ruben Garrido,
Arturo Díaz.
Cascade
Closed-Loop
Control of
Solar Trackers
Applied to
HCPV Systems.
Renewable
Energy.
(2016), Vol.
97, pp
689-696.
2.Arturo Díaz, Rubén Garrido, J.J. Soto-Bernal.
A Filtered Sun
Sensor for
Solar Tracking
in HCPV and
CSP Systems.
IEEE
Sensors
Journal.
(2019), Vol.
19, No.3, pp
917-925.

